
站内公告:
2024-06-10 05:38:05
拓扑学研究几何对象的内在的性质,具体来说就是连续形变下保持不变的性质。比如,一个皮球总是将空间分成两部分,除非你把它戳破。再比如,平面上一根橡皮筋怎么也绕不过一个钉子(即有一个洞的平面阻止曲线之间的连续变化)。
再换个角度,拓扑学主要讨论空间的分类问题。比如,为什么和
不一样,因为
抠掉一个点就变成两个不连通的部分了,而
去掉一个点仍然是连通的。为什么
和
不一样,因为
中抠掉一个点,绕这个点的橡皮筋缩不到一个点,但
是可以的。
要区分不同的几何对象或空间,就需要凭证,也就是说需要算出来一个数或一个可量化的东西,来比较它们是否一样。因此,需要有拓扑不变量的概念。我们其实是熟悉一些拓扑不变量的。比如,维度,比如凸多面体的欧拉数: 2=顶点数-边数+面数。一般的三角化曲面的欧拉数也是这么定义的,光滑曲面的欧拉数也有欧拉数,和它的三角化曲面在数值上一样。比如,凸多面体和球面的欧拉数都是2,凸多边形和圆圈的欧拉数都是0,轮胎面的欧拉数为0。
因为涉及到计算,主要有两个工具:代数拓扑或微分拓扑。代数拓扑的做法是直接将空间上的连续的问题变成代数上的计算问题,即(空间,连续映射)=> (群,同态映射)。简而言之,就是将不好计算的问题变成好计算的问题。比如,一个轮胎面有一个连通分量(0维"洞"),两个独立的闭环(1维"洞"),一个封闭的曲面(2维"洞"),这都是可以用代数拓扑中的同调代数算出来的。
神奇的是,不同维数的"洞"的个数的交错和居然等于其欧拉数:1-2+1=0。这实际上是欧拉数的一般的定义方式。比如,球面有1个连通分量(0维"泂"),0个1维"洞",1个2维"泂",于是其欧拉数为1-0+1=2。圆圈有1个连通分量(0维"洞"),1个1维"洞",于是其欧拉数为1-1=0。
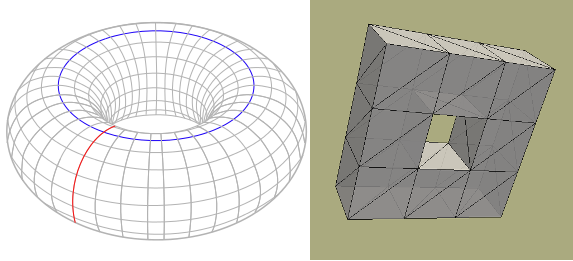
注:轮胎面有一个连通分量,2个独立的1维"洞"(红线和蓝线),1个封闭曲面,因此欧拉数定义为1-2+1=0。另一方面,它的一种三角化曲面(右图),有32个顶点,96条边,64个三角形,因此,这里的欧拉数定义为32-96+64=0。两种定义是一致的。
微分拓扑则是通过某种测量方式来测出空间上的一些局部感兴趣的东西,然后,再拼凑成全局的拓扑性质。
比如,把一个轮胎面竖起来,即在它上面定义高度函数,则此高度函数有4个点是梯度为零的点,最上面那个极大点有0个递增方向,最下面那个极小点有2个递增方向,中间两个点各有1个递增方向,将具有不同递增方向的点的个数以交错的方式相加:1-2+1=0。这其实就是轮胎面的欧拉数。这个例子可推广到一般的情况,也就是用一个好的测量方式能得到空间的拓扑性质。
总之,具体到拓扑学的各个研究领域,实际上就是找一种方法来算拓扑不变量,看一看哪些性质是不随连续形变而变的。
上面完全是以几何为背景,实际上拓扑学最初是从图论引申出来的。还需要指出来的是,数和几何是数学的两面,或看待问题的两种方式,很多情况下是可以相互转化的。
放一些图应该更好理解一些,如果有需求的话,我再整理。
Zero谈数学——聊聊拓扑(1) - DivisionByZero - 知乎专栏虽然(2)遥遥无期……但是题主可以先看着
说说个人感悟:
拓扑学其实就是研究分析学搞出来的。
请回想你初次学习数学分析时接触的是实直线连续统,在那里花了不少精力研究。
因为那时函数的定义域是取自实直线的,为了确保分析的基础,必须花精力研究实直线。
后来要对分析学进行推广(请注意数学研究中必做的事情,对现有理论进行完善推广),就提出如果函数的定义域不是实直线,比如复数,其他的空间,我们现有的理论还适用吗?对于这个问题我们显然没有底气说一定适用!因为函数的定义域是我们没见过的,不熟悉的。
基于此,我们就得系统的对它们进行研究,但我们又不可能对每一个都去研究,就抽象成一个普遍适用的来进行研究,即公理化!所以你会见到后来学过的序关系,这个是为了给任意空间中的集合定义有界用的,引入拓扑空间是为了定义开闭集(以前实直线上开闭区间的推广),有了这两样就可以推广以前的有界闭区间为紧集,然后再对分析学的三大基本定理(极值、介值、一致连续)以紧集进行推广论证,还有其他的各种推广,这样我们就逐步建立了另一种抽象的,观点更高的分析。
所谓拓扑学,很多科普文章写的是“橡皮泥几何”,其实这种比喻更适合来形容代数拓扑学。
拓扑学比较主要的三个分支是点集拓扑、代数拓扑和微分拓扑。
点集拓扑的出发点,是对微积分学里的一些基本概念,特别是对极限、连续及其相关的概念(比如开集、紧性)进行抽象,提炼出最本质的特征,相当于去皮留骨,这样就可以把这些“骨”移植到更广泛的空间上去,比如函数空间,以及更一般的拓扑空间,使得我们可以在这样的空间上定义极限和连续等概念。虽然点集拓扑学里已经给出了“同胚”的概念,但是对于一个一般的拓扑空间,我们的处理手段是相当有限(几乎为零)的——直到我们开始学习代数拓扑。
代数拓扑的工具,使得我们面对一个拓扑空间时,能够应对的手段大大拓宽了。“橡皮泥几何”指的便是“同伦变换”。通过同伦群和同调群,我们可以探测空间中的“空腔”,以及空间的拓扑“不平凡性”,尤其在处理高维空间时,同调群的计算便利性使得它比同伦群使用地更广泛一些,但是同伦群反映的信息更多一些(一分价钱一分货)。无论如何,在很多理论物理和理论经济学的抽象模型中,这些拓扑工具是很重要的。
粗略地说,微分拓扑是处理那些具有可微性的拓扑空间——光滑流形,以及大范围地定义在这些空间上的映射的学科。因此,自然地,微分拓扑是处理非线性动态系统的有力工具。比如,对于定义在整个流形上的动力系统,如果需要研究其不动点(均衡点,平衡点)的散布问题,则需要借助Morse理论和庞加莱(Poincare)与霍普夫(Hopf)的指数定理。其中,对于莫尔斯理论,其核心在于其莫尔斯不等式——这个不等式给出了光滑函数的临界点个数(这个数也被称为莫尔斯型数)的下界——这个下界由其临界点的对应维数的同调群的秩(贝蒂数)确定。同时,莫尔斯理论中的的形变定理在变分学占有重要地位,可以判断出一个非线性泛函临界点的存在性,其中一个最重要的特例,就是在偏微分方程理论中有名的山路定理。而指数定理,将不动点的个数与欧拉示性数联系起来,是一个联系分析学与拓扑学的深刻的结果,在数学史上,像这类定理一般都会得到极高的评价。最后,Morse理论现在已经被张恭庆等变分学家推广到了无穷维空间上,成为了微分拓扑学的一个“无穷维版本”,也是非线性泛函分析的重要组成部分。
拓扑学的内核是几何学。
在欧氏几何中,刚性运动保持内积不变:即平移、旋转、翻折保持长度、角度不变;仿射几何中仿射变换则是保持单比、面积比不变;射影几何中射影变换则是保持交比不变……几何学的精神就是研究几何对象在特定变换下的不变性。这也就是菲利克斯·克莱因在1872年发表的爱尔兰根纲领中的思想。
那么沿着这个思路,拓扑学研究的就是——在连续映射下保持不变的性质。上面提及的变换、映射都是连续变换,它们为我们研究各种连续变换提供了丰富的例子。连续变换可以说是几何学中最为一般的变换,它可能不会保持长度,也可能不会保持比例……但是几何对象在任意连续映射下,总有些本质是不变的。
了解拓扑学的前提,首先我们要对连续性有一定的了解。当然,我不可能直接将定义怼到读者脸上,对连续性的感性认知,人人生而就有。不过我在此拙劣地尝试去表述它:两个原本很近的点,经过连续映射后,它们的像点也很近。
我这里用了“近”这个感性的描述,事实上暗示了(拓扑)空间可能存在度量。诚然,度量诱导拓扑是十分自然的事情,足以应对常见的情形,但是数学家依然不满足,因为“远近”的概念还是没有摆脱欧氏空间给我们带来的束缚;邻域,则是从最基本的点集出发,为我们提供了对于“近”这一概念更一般性的刻画。我们最常见的邻域是度量空间中的开球。
邻域,简单来说就是描述一个(拓扑)空间的点是以什么样的方式聚集在一起的。它们被一份一份地打包起来,而连续映射其实是这些“包裹”的快递员。快递打包的灵活性,取决于邻域的丰富性。邻域就像是泡泡,两个泡泡并集是一个大的泡泡,两个泡泡交集会产生一个小泡泡。这些泡泡都可以作为快递的包裹外套。(我讲个泡泡啊!!!)
包裹从一个空间快递到另一个空间是不能“打散”的,打散则就意味着连续性的破坏。每一个完好无损被邮递过来的包裹,一定原先也是完好无损的,这就是连续性。
如果两个空间存在一个连续映射,其逆映射也连续,我们就说两者同胚。同胚就意味着两者的一切拓扑性质都相同:
同胚,那么从
出发到任意其他的拓扑空间
的连续映射,都自然对应一个从
到
的连续映射(上图红色箭头)
;反过来,如果
到
的有一个连续映射,那么一定有一个从
到
的映射。按范畴论的思想,这
并无本质区别,可以视为同一个对象(设想两个人的人际关系网完全一样,那么这两个人的社会身份是一样的,即人是社会关系的总和)。
将一个正方形压扁成一根线段是连续映射,但是这个映射不是同胚映射,显然它不可逆。从图形角度看这个“压扁映射”,它之所以不是同胚,是因为它将原来的点的邻域直接降维了,科幻小说《三体》中用二向箔降维打击太阳系,我想哪一天外星文明想还原太阳系,基本上是不可能的事情。
虽然正方形和线段不同胚,但是两者同伦。同伦是一个随时间变量变化的连续变形,同伦允许将对象“压扁”。事实上,同胚映射要求太高了,哪怕建立同伦也是十分困难的事情。

甜甜圈同胚于咖啡杯,因为两者的亏格都是1。如果在游泳圈(空心)表面挖去一个圆盘呢?它同胚于何物?上图为我们展示了这个连续变化的过程,其同胚型是两个平环在一个正方形区域粘贴重合。如果求其同伦型,则可以继续压缩变细,最终成为两个圆周的一点并。
不变量其实是为了分类。
同胚(同伦、同调)显然是一个等价关系,彼此不同胚的拓扑空间,它们注定有质的区别。闭曲面分类定理告诉我们,这个区别就在于“洞”的个数,称之为亏格。对于低维空间,这都是显而易见的,那如何探讨更高维的不变量呢?
与此同时,数学家不再满足“不变量”,谁说不变量非得是个数呢?拓扑空间是否可以用其所蕴含的群作为名片?代数和拓扑应运而生。
例如由拓扑空间上道路的接续作为乘法而构成的群——基本群,由闭链的形式和所构成的交换群——同调群……这些群的定义不受维数的影响,是研究高维拓扑空间的利器。事实上,拓扑空间各个维数同调群的秩的交错和,恰恰等于欧拉示性数,而后者与亏格有关。回忆黄金多面体的欧拉公式:
这是一个交错和的形式。这里的 就是球面的欧拉示性数,因为黄金多面体和球面同胚。
到目前为止,就连关于高维球面的同伦群(稳定同伦群理论)仍然由许多未解之谜,数学家为此开发了许多代数拓扑工具:同调代数、谱序列、同伦论……
正如前文所述,一般的拓扑空间可能都不具备度量。但是如果想将分析的工具应用在拓扑学中,我们不得不对拓扑空间的光滑性有一定要求,我们称之为微分拓扑流形。
流形上的向量场是切丛的截面。所谓切丛由流形每一点的切空间(切线、切平面、……)构成。Hopf-Poincare定理告诉我们,流形上向量场的所有奇点指数,与流形的欧拉示性数有关。而Morse理论则告诉我们,通过流行嵌入到欧氏空间中的高度函数的非退化临界点,可以决定流形生长的细节——在哪里分叉,在哪里闭合,于是其同伦型也就被决定了。
仅仅是研究切丛就获得了如此丰富的信息,著名的Gauss-Bonnet-Chern(陈省身)定理更是暗示流形的纤维丛蕴藏着更丰富信息……
相关推荐: