焦点注册

焦点资讯

当前位置：首页 > 焦点资讯

流形优化方法求解约束问题

2024-04-07 23:23:20

最近几年，流形优化方法（或者叫黎曼优化）算是比较热门的，它提供了一个新的角度去求解和分析一类特殊的约束优化问题，也就是流形约束优化问题。

这篇文章的目的是让大家对这个方向有个大概的理解。详细的入门书籍建议看【1】【2】

另外综述文章看【3】还有一些博士论文：【4】【5】.

一句话概括就是：传统的优化方法是在欧氏空间考虑问题，而流形优化是在黎曼流形中考虑问题，这个黎曼流形哪来的呢？约束给的！也就是把欧氏空间的约束看成是一个流形。

1.问题阐述

流形约束优化问题是指一类特殊的约束优化问题，它的约束具有流形结构。考虑一般的问题：

$\\begin{split}\\min_x & f(x) ,~~\\mbox{s.t. }x\\in\\mathcal{M}. \\end{split}\\\\$ 其中 $\\mathcal{M}$ 表示流形约束。这个问题你可以简单的把它看成是约束问题，然后用传统的一些针对约束优化问题的优化方法去求，比如罚方法，增广拉格朗日方法等等。为什么有了这些方法还有去弄个流形优化方法出来，因为首先流行约束通常非凸，收敛性很难保证，其次这些方法不能保证迭代点总是满足约束，最后，流形约束是有结构的，这些方法没有去探索这些结构信息。以上说的三点正是流形优化的三个优点：

所有迭代点保持约束可行性，也就是总是在流形 $\\mathcal{M}$ 上。
流形优化将问题（1）理解为流形上的无约束优化问题，便于分析收敛性。
利用了流形约束本身的结构信息。

2.流形约束的例子

接下来介绍一下常见的 $\\mathcal{M}$ 有哪些

Stiefel manifold: $\\mbox{St}(p,n)=\\{X\\in\\mathbb{R}^{n\ imes p}| X^TX=I_p\\}$
Grassmann manifold: $\\mbox{Gr}(p,n)$ :all $p$ -dimensional subspaces of $\\mathbb{R}^n$
Symmetric positive definite manifold: $S_{++}(r)=\\{X\\in\\mathbb{R}^{r\ imes r}| X^T=X,X\\succ 0\\}$
Fixed-rank manifold: $\\mathbb{R}^{m\ imes n}_r=\\{X\\in\\mathbb{R}^{m\ imes n}| \\mbox{rank}(X)=r\\}$

3.问题的例子

稀疏主成分分析

$\\begin{equation}\\label{chap1.2-matspca}\\left\\{ \\begin{split}\\min_{X\\in\\mathbb{R}^{n\ imes r}}& -tr(X^TA^TAX) + \\mu \\|X\\|_1, \\\\ \\mbox{s.t. }~~ & X^TX=I_r. \\end{split}\\right. \\end{equation}\\\\$

Finding the sparsest vector in subspace

$\\begin{equation}\\min_x \\|Qx\\|_1, ~~ \\mbox{s.t. }x^Tx=1, \\end{equation}\\\\$

典型相关性分析

$\\begin{equation}\\label{chap1.2-cca}\\left\\{ \\begin{split}\\max_{u, v}~& u^{T}X^{T}Yv, \\\\ \\mbox{s.t.}& \\quad u^{T}X^{T}Xu=1, v^{T}Y^{T}Yv=1. \\end{split}\\right. \\end{equation}\\\\$

鲁棒低秩矩阵恢复

$\\begin{equation}\\begin{split}\\min_X & \\|P_{\\Omega}(X-M)\\|_1 \\\\ \\mbox{s.t.}& X\\in\\mathcal{M}_r:=\\{X | \\mbox{ rank }(X)=r\\}\\end{split}\\end{equation}\\\\$

在欧氏空间中的优化方法已经很成熟，对于在流形上设计优化方法，一切在欧氏空间中看起来理所应当的东西在黎曼流形上却不成立，因此我们需要重新定义。

1.黎曼流形

引用wen huang的一句话解释：

"Roughly, a Riemannian manifold $\\mathcal{M}$ is a smooth set with a smoothly-varying inner product on the tangent spaces."

2.黎曼梯度

因为我们要设计优化方法，梯度是最重要的，我们要定义流形上的梯度，称为黎曼梯度，并且限制在切空间上。

Riemannian Gradient: $\\mbox{grad}f(x) \\in T_x\\mathcal{M}$ is denoted as the unique tangent vector satisfying

$\\left< \\mbox{grad}f(x), \\xi \\right>_x=df(x)[\\xi], \\mbox{ for any }\\xi\\in T_x\\mathcal{M}. \\\\$

为什么要在切空间上考虑梯度，因为切空间是线性子空间，性质好。可以将切空间理解为流形在某个点的线性逼近，因此只要邻域足够小，切空间和流形的差可以得到控制。

3.收缩算子

有了负梯度，接下来是怎么往前走一步，假设我们有了 $x^k\\in \\mathcal{M}$ ，和该点的黎曼梯度： $\\mbox{grad}f(x^k)$ ，我们如何得到 $x^{k+1}\\in \\mathcal{M}$ ，如果是像欧氏空间一样：

$x^{k+1}=x^k - \\alpha \\mbox{grad}f(x^k) \\\\$ 这不能保证迭代点还在流形上，也就是说不满足约束条件。因此我们定义流形上的”加法“：

Retraction：A retraction on a manifold $\\mathcal{M}$ is a smooth mapping $R:T\\mathcal{M}\\rightarrow \\mathcal{M}$ with the following properties. Let $R_x:T_x\\mathcal{M}\\rightarrow \\mathcal{M}$ denote be the restriction of $R$ to $T_x\\mathcal{M}$ ：

$R_x(0_x)=x$ , where $0_x$ the zero element of $T_x\\mathcal{M}$
$dR_x(0_x)=id_{T_x\\mathcal{M}}$ ,where $id_{T_x\\mathcal{M}}$ is the identity mapping on $T_x\\mathcal{M}$

对于不同的流形有不同的收缩算子，并且对于某个流形可以有多个算子。在欧氏空间中，收缩算子就是传统意义下的加法。

有了这两个定义，我们就可以很轻松的设计出黎曼梯度方法，基本迭代为：

$x_{k+1}=R_{x_k}(-\\alpha_k\\mbox{grad}f(x_k)) \\\\$

我们来比较下传统梯度和黎曼梯度的区别：

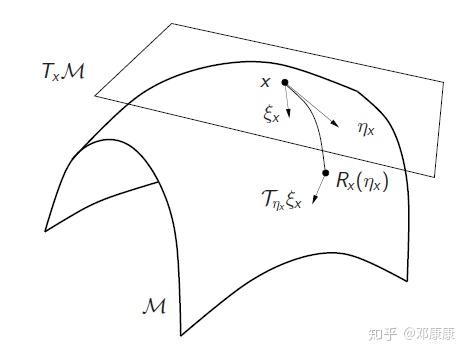
4.向量转移算子

在黎曼流形中，不同点的梯度位于该点的切空间上，那么问题来了，不同点的黎曼梯度如何去比较？比如 $\\mbox{grad}f(x^k)$ 和 $\\mbox{grad}f(x^{k+1})$ ,这两个不在同一个切空间上。这里的解决方案是，我们把其中一个”平移“到另一个的切空间上。于是有了这个算子：

这个算子在共轭梯度方法中会用到。

1.黎曼梯度方法

$x_{k+1}=R_{x_k}(-\\alpha_k\\mbox{grad}f(x_k)) \\\\$

和传统梯度方法一样，其中的步长可以有不同的选择，比如线搜索，BB步长等

2.黎曼共轭梯度

$\\left\\{ \\begin{split}x^{k+1}&=R_{x^k}(\\alpha_k \\eta^k) \\\\ \\eta^{k+1}&=-\\mbox{grad}f(x^{k+1}) + \\beta_{k+1}\\mathcal{T}_{\\alpha_k \\eta^k}(\\eta^k ) \\end{split}\\right. \\\\$

注意到第二步，因为 $\\mbox{grad}f(x^{k+1}) \\in T_{x^{k+1}}\\mathcal{M}$ 和 $\\eta^k \\in T_{x^k}\\mathcal{M}$ 不在同一个切空间上，没办法作比较，所以我们对 $\\eta^k$ 用了向量转移算子，使得他们保持在同一个切空间。

二阶方法比较复杂一点，下次再补上。

流形优化用于求解一类约束优化问题，将欧氏空间中的约束优化问题转化为黎曼流形上的无约束优化问题。关于欧氏空间下优化理论的很多东西都能扩展过来，比如函数的凸性，光滑性等等。

流形优化方法并不能求解所有的约束优化，只限于那些可以看成是黎曼流形的约束，比如前面提到的正交约束，对称正定约束，低秩约束等等。
欧氏空间的临近类算法不太好扩展到黎曼流形，至少在计算方面，因为在欧氏空间下“临近友好”这个性质扩展到黎曼流形下就没有了。

我的专栏

凸优化算法与理论黎曼优化

【1】 Absil, P-A., Robert Mahony, and Rodolphe Sepulchre.Optimization algorithms on matrix manifolds. Princeton University Press, 2009.

【2】Nicolas Boumal. An introduction to optimization on smooth manifolds. 2020.

【3】Hu, Jiang, Xin Liu, Zai-Wen Wen, and Ya-Xiang Yuan. "A brief introduction to manifold optimization."Journal of the Operations Research Society of China(2019): 1-50.

【4】Zhang, Hongyi. "Topics in non-convex optimization and learning." PhD diss., Massachusetts Institute of Technology, 2019.

【5】Huang, Wen. "Optimization algorithms on Riemannian manifolds with applications." (2013).

上一篇：抖音新手如何快速开通商品橱窗，新手开通抖音橱窗怎么操作

下一篇：[译]优化 MP4 视频以获得更快的流传输速度

【返回列表】